很多人都不明白什么是Monad，并不是因为不会用，不知觉可能就在用某种 monad。 定义和使用起来其实不难，困惑的大多应该是后面的这堆理论– 范畴论。当然，我也没学过范畴论，只是略微看得懂写Haskell罢了。

我也画过一些图来解释，又会被嫌弃画风不好。但是，作为灵魂画师，我只 是觉得自己萌萌的啊 在乎画的灵魂是否能够给你一点启发。好吧，讲这么学术的东西，还是用dot来画吧，看起来好正规呢。

好了，安全带系好，我真的要开车了。为了 防止鄙视链顶端的语言用户们喷再嫌弃 解释的不到位，就用 Haskell 好了（虽然haskell也没到鄙视链顶），其实也不难解释清楚 才怪 。

这里面很多很装逼的单词，它们都是 斜体 ，就算没看懂，把这些词记住也足够装一阵子逼了买一阵子萌了。

第一部分：范畴论Catergory Theory

Category

一个 范畴Category 包含两个玩意

• 东西 O （Object）
• 两个东西的关系，箭头 ~> （ 态射Morphism ）

一些属性

• 一定有一个叫 id 的箭头，也叫做 1
• 箭头可以 组合 compose

恩，就是这么简单

这些玩意对应到 haskell 的 typeclass 大致就是这样

class Category (c :: * -> * -> *) where
  id :: c a a
  (.) :: c y z -> c x y -> c x z

注意到为什么我会箭头从右往左，你会发现这个方向跟 compose 的方向刚好一致

如果这是你第一次见到 Haskell 代码，没有关系，语法真的很简单 才怪

• class 定义了一个 TypeClass， Category 是这个 TypeClass 的名字
• Type class 类似于定义类型的规范，规范为 where 后面那一坨
• 类型规范的对象是参数 (c:: * -> * -> *) ， :: 后面是c的类型
• c 是 higher kind ，跟higher order function的定义差不多，它是接收类型，构造新类型的类型。这里的 c 接收一个类型，再接收一个类型，就可以返回个类型。
• id:: c a a 表示 c 范畴上的 a 到 a 的箭头
• . 的意思 c 范畴上，如果喂一个 y 到 z 的箭头，再喂一个 x 到 y 的箭头，那么就返回 x 到 z 的箭头。

简单吧hen nan ba?还没有高数抽象呢。

Hask

Haskell 类型系统范畴叫做 Hask

在 Hask 范畴上：

• 东西是类型
• 箭头是类型的变换，即 ->
• id 就是 id 函数的类型 a -> a
• compose 当然就是函数组合的类型

type Hask = (->)
instance Category (Hask:: * -> * -> *) where
  (f . g) x = f (g x)

我们看见新的关键字 instance ，这表示 Hask 是 Type class Category 的实例类型，也就是说我们可以Hask的个构造器去真的构造一个类型

比如：

(->) a a

就构造了一个从a类型到a类型的的类型

构造出来的这个类型可以作为 id 函数的类型

id :: (->) a a

Duel

每个 Category还有一个镜像，什么都一样，除了箭头是反的

函子 Functor

两个范畴中间可以用叫 Functor 的东西来连接起来，简称 T。

所以大部分把Functor/Monad比喻成盒子其实在定义上是错的，虽然这样比喻比较容易理解，在使用上问题也不大。但是，Functor只是从一个范畴到另一个范畴的映射关系而已。

• 范畴间 东西的 Functor 标记为 T(O)
• 范畴间 箭头的 Functor 标记为 T(~>)
• 任何范畴C上存在一个 T 把所有的 O 和 ~> 都映射到自己，标记为id functor 1_C
  • 1_C(O) = O
  • 1_C(~>) = ~>

class (Category c, Category d) => Functor c d t where
  fmap :: c a b -> d (t a) (t b)

Functor c d t 这表示从范畴 c 到范畴 d 的一个 Functor t

如果把范畴 c 和 d 都限制到 Hask 范畴

class Functor (->) (->) t where
  fmap :: (->) a b -> (->) (t a) (t b)

-> 在 Haskell 中是中缀类型构造器，所以是可以写在中间的

这样就会变成我们熟悉的 Funtor 的 Typeclass（把Functor 的第一第二个参数去掉的话）

class Functor t where
  fmap :: (a -> b) -> (t a -> t b)

而 自函子endofunctor 就是这种连接相同范畴的 Functor，因为它从范畴 Hask 到达同样的范畴 Hask

这里的 fmap 就是 T(~>)，在 Hask 范畴上，所以是 T(->), 这个箭头是函数，所以也能表示成 T(f) 如果 f:: a -> b

Cat +猫+

当我们把一个Category看成一个object，functor看成箭头，那么我们又得到了一个Category，这种object是category的category我们叫它 – Cat

已经没法讲了，看 TODO 图吧

自然变换Natural Transformations

Functor 是范畴间的映射，而 Functor 在 Cat 范畴又是个箭头，所以，Functor间的映射，也就是 Cat 范畴上的 Functor，叫做 自然变换

所以范畴 c 上的函子 f 到 g 的自然变化就可以表示成

type Nat c f g = c (f a) (g a)

Hask 范畴上的自然变化就变成了

type NatHask f g = f a -> g a

有趣的是，自然转换也满足箭头的概念，可以当成 functor 范畴上的箭头，所以又可以定义出来一个 Functor Catergory

• 东西是函子
• 箭头是自然变换

要成为范畴，还有两点

• id 为 f a 到 f a 的自然变换
• 自然变换的组合

我们来梳理一下，已经不知道升了几个维度了，我们假设类型是第一维度

• 一维： Hask， 东西是类型，箭头是 ->
• 二维： Cat， 东西是 Hask， 箭头是 Functor
• 三维： Functor范畴， 东西是Functor， 箭头是自然变换

感觉到达三维已经是极限了，尼玛还有完没完了，每升一个维度还要起这么多装逼的名字，再升维度就要一脸懵逼了呢。虽然维度不算太高，但是已经不能用简单的图来描述了，所以需要引入 String Diagram。

String Diagram

String Diagram 的概念很简单，就是点变线线变点。

当有了自然变换之后，没法表示了呀，那原来的点和线都升一维度，变成线和面，这样，就腾出一个点来表示自然变换了。

compose的方向是从右往左，从下到上。

Adjunction Functor 伴随函子

范畴C和D直接有来有回的函子，为什么要介绍这个，因为它直接可以推出 Monad

让我们来看看什么叫有来回。

其中：

• 一个范畴 C 可以通过函子 G 到 D，再通过函子 F 回到 C，那么 F 和 G 就是伴随函子。
• η 是 GF 到 1_D 的自然变换
• ε 是 1_C 到 FG 的自然变换

同时根据同构的定义，G 与 F 是 同构 的。

同构指的是若是有

f :: a -> b
f':: b -> a

那么 f 与 f' 同构，因为 f . f' = id = f' . f

伴随函子的 FG 组合是 C 范畴的 id 函子 F . G = 1_c

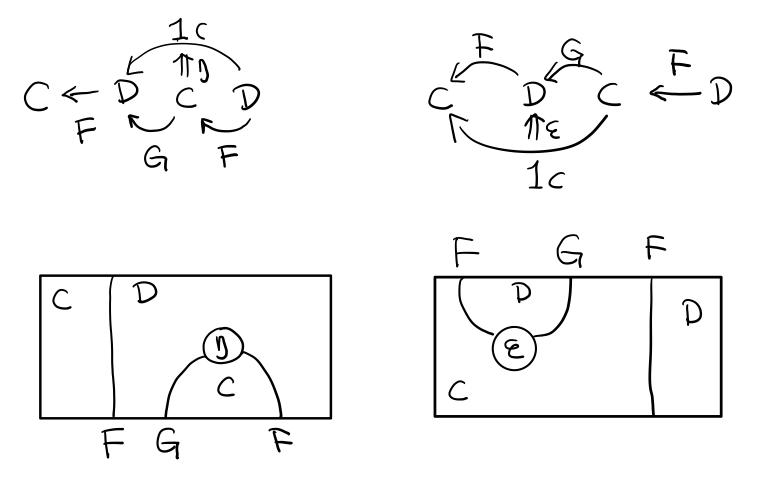
Functor 不仅横着可以组合，竖着(自然变换维度)也是可以组合的，因为自然变换是 Functor 范畴的箭头。

当到组合 F η . ε F 得到一个弯弯曲曲的 F 时，我们可以拽着F的两段一拉，就得到了直的 F。

String Diagram 神奇的地方是所有线都可以拉上下两端，这个技巧非常有用，在之后的单子推导还需要用到。

从伴随函子到 单子 Monad

有了伴随函子，很容易推出单子，让我们先来看看什么是单子

• 首先，它是一个 endofunctor T
• 有一个从 i_c 到 T 的自然变化 η (eta)
• 有一个从 T² 到 T 的自然变化 μ (mu)

class Endofunctor c t => Monad c t where
  eta :: c a (t a)
  mu  :: c (t (t a)) (t a)

同样，把 c = Hask 替换进去，就得到更类似我们 Haskell 中 Monad 的定义

class Endofunctor m => Monad m where
  eta :: a -> (m a)
  mu :: m m a -> m a

要推出单子的 η 变换，只需要让 FG = T

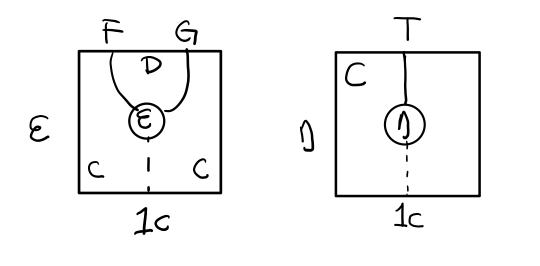
同样的，当 FG = T, F η G 就可以变成 μ

三角等式

三角等式是指 μ . T η = T = μ . η T

要推出三角等式只需要组合 F η G 和 ε F G

换到代码上来说

class Endofunctor m => Monad m where
  (mu . eta) m = m

同样的，左右翻转也成立

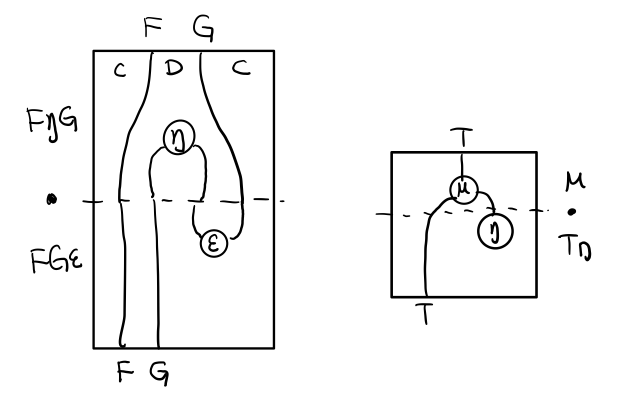
T η 就是 fmap eta

(mu . fmap eta) m = m

如果把 mu . fmap 写成 >>= , 就有了

m >>= eta = m

结合律

单子另一大定律是结合律，让我们从伴随函子推起

假设我们现在有函子 F η G 和 函子 F η G F G, compose 起来会变成 F η G . F η G F G

用 F G = T ， F η G = μ 代换那么就得到了单子的 μ . μ T

当组合 F η G 和 F G F μ G 后，会得到一个镜像的图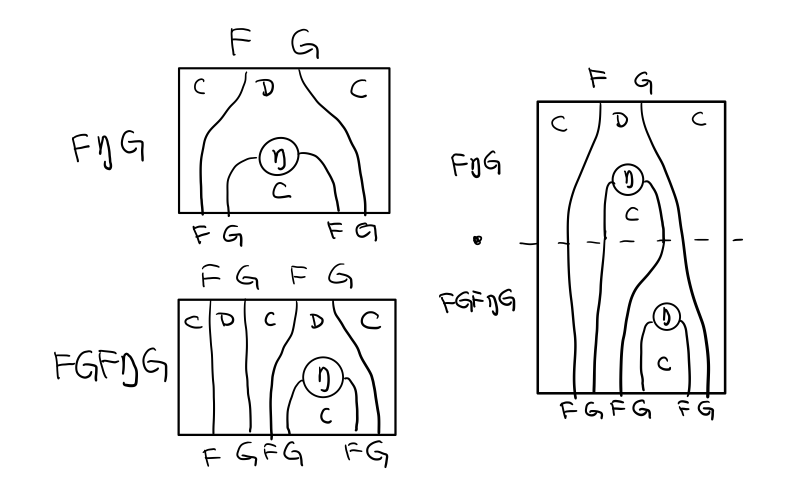

对应到单子的 μ . T μ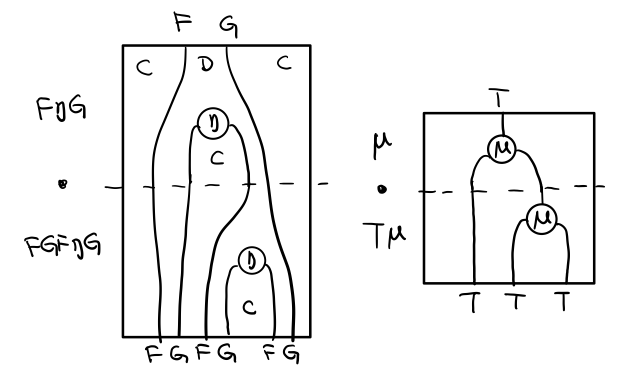

结合律是说 μ . μ T = μ . T μ , 即图左右翻转结果是相等的，为什么呢？看单子的String Diagram 不太好看出来，我们来看伴随函子

如果把左图的左边的 μ 往上挪一点，右边的 μ 往下挪一点，是不是跟右图就一样了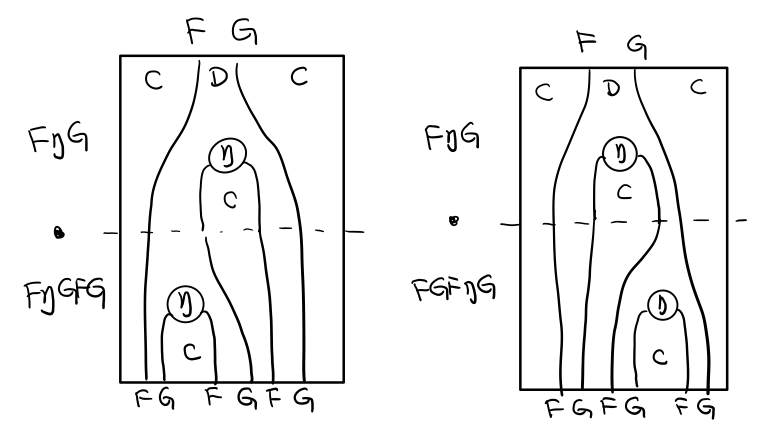

结合律反映到代码中就是

mu . fmap mu = mu . mu

代码很难看出结合在哪里，因为正常的结合律应该是这样的 (1+2)+3 = 1+(2+3)，但是不想加法的维度不一样，这里说的是自然变换维度的结合，可以通过String Diagram 很清楚的看见结合的过程，即 μ 左边的两个T和先 μ 右边两个 T 是相等的。

Yoneda lemma / 米田共 米田引理

米田引理是说所有Functor f a 一定存在 embed 和 unembed，使得 f a 和 (a -> b) -> F b isomorphic 同构

haskell还要先打开 RankNTypes 的 feature

{-# LANGUAGE RankNTypes #-}

embed :: Functor f => f a -> (forall b . (a -> b) -> f b)
embed x f = fmap f x

unembed :: Functor f => (forall b . (a -> b) -> f b) -> f a
unembed f = f id

embed 可以把 functor f a 变成 (a -> b) -> f b

unembed 是反过来， (a -> b) -> f b 变成 f a

上个图就明白了

Rank N Type

• Monomorphic Rank 0 / 0级单态: t
• Polymorphic Rank 1 / 1级 变态 多态: forall a. a -> t
• Polymorphic Rank 2 / 2级多态: (forall a. a -> t) -> t
• Polymorphic Rank 3 / 3级多态: ((forall a. a -> t) -> t) -> t

看rank几只要数左边 forall 的括号嵌套层数就好了

一级多态锁定全部类型变化中的类型a

二级多态可以分别确定 a -> t 这个函数的类型多态

比如

rank2 :: (forall a. a -> a) -> (Bool, Char)
rank2 f = (f True, f 'a')

• f 在 f True 时类型 Boolean -> Boolean 是符合 forall a. a->a 的
• 在 f 'a' 时类型是 Char -> Char 也符合 forall a. a->a

但是到 rank1 类型系统就懵逼了

rank1 :: forall a. (a -> a) -> (Bool, Char)
rank1 f = (f True, f 'a')

f 在 f True 是确定 a 是 Boolean，在rank1多态是时就确定了 a->a 的类型一定是 Boolean -> Boolean

所以到 f 'a' 类型就挂了。

Kleisli Catergory

Functor 的 Catergory 叫做 Functor Catergory，因为有箭头 – 自然变换。Monad 也可以定义出来一个 Catergory（当然由于Monad是 Endofunctor，所以他也可以是 自函子范畴），叫做 Kleisli Catergory，那么 Kleisli 的箭头是什么？

我们看定义，Kleisli Catergory

1. 箭头是 Kleisli 箭头 a -> T b
2. 东西就是c范畴中的东西. 因为 a 和 b 都是 c 范畴上的， 由于T是自函子，所以 T b 也是 c 范畴的

看到图上的 T f fmap f 和 μ 了没？

f :: b -> T c
fmap f :: T b -> T^2 c
mu :: T^2 c -> T c

紫色的箭头连起来（compose）就是 T f'，所以,

tb >>= f = mu . fmap f tb

大火箭则是蓝色箭头的组合

(f <=< g) = mu . T f . g = mu . fmap f . g

而且大火箭就是 Kleisli 范畴的 compose

(<=<) :: Monad T => (b -> T c) -> (a -> T b) -> (a -> T c)

Summary

第一部分理论部分都讲完了， 如果你读到这里还没有被这些吊炸天乱七八糟的概念搞daze，接下来可以看看它到底跟我们编程有鸟关系呢？第二部分 -> 处基猫呢，将介绍由这些概念产生的一些实用的初级monad。